LA DIFERENCIAL

La diferencial

Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.

DEFINICION Y EJEMPLOS
Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.

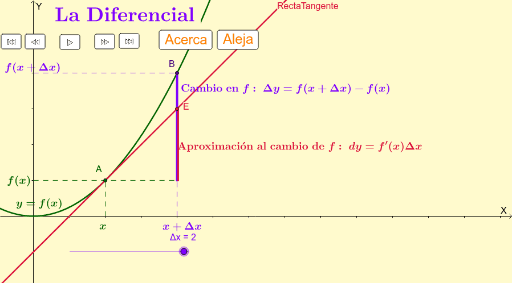
 El diferencial dy se define en cursos introductorios mediante la expresión:

${\displaystyle dy=f'(x)\,dx,}$

donde ${\displaystyle f'(x)}$ es la derivada de f con respecto a x, y donde dx es una variable real adicional (de manera que dy es una función de dos variables x, y dx). La notación es tal que la expresión:

${\displaystyle dy={\frac {dy}{dx}}\,dx}$

donde la derivada es representada en la notación de Leibniz dy/dx, se mantiene, y es consistente con respecto a la derivada como el cociente de diferenciales.

El significado preciso de las variables dy y dx depende del contexto de aplicación y del nivel de rigor matemático requerido. Según consideraciones matemáticas rigurosas modernas, las notaciones dy y dx son simplemente variables reales y son manipuladas como tales. El dominio de estas variables puede tomar un significado geométrico particular si el diferencial es considerado como una forma diferencial, o significado analítico si el diferencial es considerado como una aproximación lineal al incremento de una función. En aplicaciones físicas, a menudo, se requiere que las variables dx y dy sean sumamente pequeñas (infinitesimales).